The frequency range where room modes are dominating is below the Schroeder frequency and can be obtained by using the following formula to calculate the crossover frequency between the discrete room modes and the irregular spaced higher frequencies:
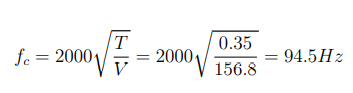
The crossover frequency fc defines a transition zone and will not be a definite limit. The Calculation of the Schroeder frequency is based on reasonable reverberation times, a diffuse sound field, and an unobstructed interior. This leads to an error in the calculation since these requirements will not apply to small rooms. The dominance of room modes will most likely be higher than the calculated 94.5 Hz.
The axial room modes up to the crossover frequency are listed in table 1
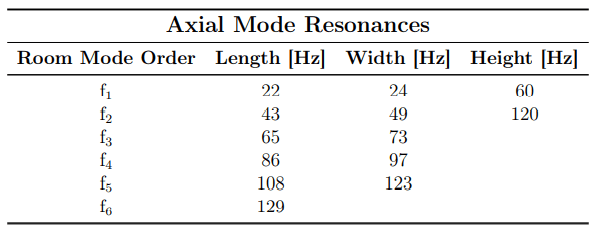
forth-order room mode
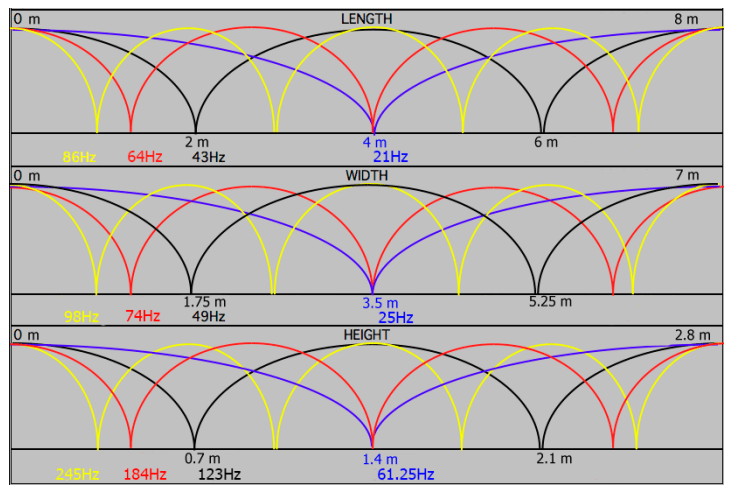
Figure 1. illustrates the room mode distribution for the first four mode orders. The first and third-order room modes will not be problematic for listeners approaching the null of these modes. This will be the case at seated ear height of ± 1.4 m whereas the second-order room mode shows its pressure peak and has to be addressed by other means.
The average axial mode spacing is around 9.2 Hz with a standard deviation of 5.58 Hz. This may be considered to be a close mode spacing and also might result in overall smoother frequency response due to overlapping room modes. A room mode exhibits a resonance curve with a certain bandwidth that is dependent on the reverberation time of a room. The bandwidth of a room resonance can be calculated by using the following expression:
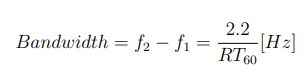
where reverberation times of 0.2 to 0.5 seconds will cause room resonances with a bandwidth ranging from 4.4 to 11 Hz, leading to the conclusion that the bandwidth of the resonance peak increases with lower reverberation times.
Overlapped Room modes
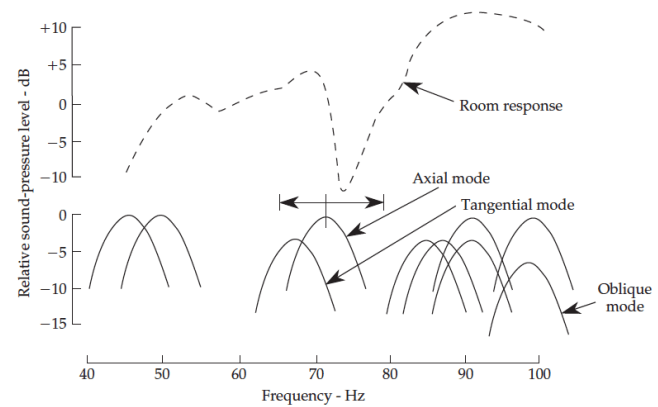
A scheme of overlapping room modes is illustrated in figure 2. It can be seen that the several overlapping resonances cause an overall sound pressure contour which is dependent on the overlapping mode bandwidth. Whereby resulting narrow dips can be neglected since they are less noticeable as concluded by Buchlein (cited in Toole 445). Another effect of mode overlapping has to be considered in terms of room mode interaction. The excitation of one resonance will force adjacent room modes into excitation which results in an energy boost within a wider frequency range.
In this post, we went to the Room Mode Calculation and examined its considerations. Items needed to mention audio improvements and other parameters will be published in future posts. These items will pave the way for creating a home theater with the highest quality.
The audio products offered in Saba intelligent systems, which include professional speakers and amplifiers and inakustik cables with their great variety and high quality, make it possible to implement any type of equipment according to the relevant needs.



